De la génération des fractales
Théorie et Applications

John Bonobo
PhD Applied Mathematics
Bonobo Future Systems Inc. - Nancy, Berlin, 2000-2004.

Table des matières


Notations

1. Introduction


2. Construction d'un ensemble fractal par itération d'une fonction complexe

2.1. Construction théorique, définitions et propriétés élémentaires
2.1.1. Orbites et ensemble fractal
2.1.2. Stabilité des orbites
2.2. Quelques exemples
2.2.1. Les fractales de Mandelbrot et de Julia
2.2.1.1. Description fine des ensembles de Mandelbrot et de Julia
2.2.1.1.1 Propriétés élémentaires des Julia et du Mandelbrot
2.2.1.1.2 Connexité des Julia et lien avec le Mandelbrot
2.2.1.1.3 Périodes des bulbes du Mandelbrot
2.2.1.1.4 Quelques points remarquables de l'ensemble de Mandelbrot
2.2.1.1.5 Quelques ensembles de Julia remarquables
2.2.1.2. Un premier algorithme pour tracer les Julia : La méthode d'itération inverse (ou d'orbite inverse)
2.2.2. Les fractales de Mandelbrot et Julia généralisées
2.2.3. Les fractales de Newton
2.3. Algorithmes de représentation
2.3.1. Premier temps de sortie
2.3.2. Estimateurs de distance
2.3.3. Temps d'entrée (ou pièges à orbites)
2.3.4. Angle de sortie, courbure
2.3.5. Statistiques
2.3.6. Suites de Cauchy et orbites périodiques
2.3.7. Densité des orbites

3. Les fractales de Lyapunov

3.1. Formule d'itération
3.2. Exposant de Lyapunov

4. Transformations du plan

4.1. Effet de loupe gaussienne
4.2. Inversion du plan complexe
4.3. Projection sur la sphère de Riemann

Références

Notations

L'emploi du HTML rend problématique l'affichage de certains symboles mathématiques, par simplicité nous utiliserons les notations suivantes :

N Ensemble des entiers naturels : 0,1,2,3,...
R Ensemble des nombres réels
Rd Espace euclidien à d dimensions
C Ensemble des nombres complexes (de la forme z = x + iy, avec x et y dans R et i2= −1)
  
Dans tout ce texte on ne fera pas la distinction entre l'ensemble R2 et le plan complexe C, autrement dit on assimile tout couple (x,y) ∈ R2 au nombre complexe z = x + iy ∈ C correspondant. On ne refera pas la théorie des nombres complexes, qui permettent ici une écriture plus naturelle et plus simple des formules.

√  x 
 Racine carrée de x
||(x,y)|| Norme du vecteur (x,y)∈R2, autrement dit la distance entre (x,y) et l'origine (0,0). 
Par le théorème de Pythagore, ||(x,y)|| =  √  x2 + y2 .
z Complexe conjugué de z : si z = x + iy alors z = x − iy.
|z| Module du nombre complexe z : si z = x + iy alors |z|=||(x,y)||.
∞ Infini
f(n)(x)  f itérée n fois : f(n)(x)=f(f(f(...f(x)...)))
  
F Ensemble fractal générique
M Ensemble fractal de Mandelbrot
J(C) Ensemble fractal de Julia "plein" (de paramètre C dans C)
N(P) Ensemble fractal de Newton (associé au polynome complexe P)

Rappels sur les nombres complexes :
On introduit le nombre "imaginaire" i tel que i2= −1.

Forme cartésienne :
z = x + i y avec x et y dans R.
x est la partie réelle de z et y la partie imaginaire de z.

Forme polaire : (on mesure ici les angles en radians, on rappelle que π radians = 180 degrés)
z = r eiθ avec r > 0 et θ∈[0;2π[.
r est le module ou la norme de z (notée |z|) et θ l'argument de z.

Passage d'une forme à l'autre :
On a eiθ = cos(θ) + i sin(θ) (formule d'Euler), d'où
x = r cos θ et y = r sin θ.
D'autre part, grâce au théorème de Pythagore,
r = |z| =  √  x2 + y2 
et, dans un triangle rectangle la tangente est le rapport entre le coté adjacent et le coté opposé à l'angle droit, autrement dit tg(θ)=y/x, donc en tenant compte de l'orientation et en traitant à part le cas x=0,
si x ≠ 0 :     θ = arctg (y/x) si x > 0
θ = arctg (y/x) +π     si x < 0
 
si x = 0 : θ = π/2 si y > 0
θ = 3π/2 si y < 0.


 Représentation cartésienne et polaire d'un nombre complexe

Représentation cartésienne et polaire d'un nombre complexe z
Règles de calcul :
Soient z = x + i y = r eiθ et z′ = x′ + i y′ = r′ eiθ′.

Addition : z + z′ = (x + x′) + i(y + y′)
Multiplication : z z′ = (x x′ − y y′) + i(x y′ + x′ y) = r r′ ⋅ ei(θ + θ′)
Division : z/z′ = (x x′ + y y′)/(x′2 + y′2) + i(&minus x y′ + x′ y)/(x′2 + y′2) = r/r′ ⋅ ei(θ - θ′)
Puissance : zz′ = e z′(log r + iθ) = e x′ log r − y′ θ [ cos (x′ θ + y′ log r ) + i sin (x′ θ + y′ log r ) ]

2.2. Quelques exemples

2.2.1. Les fractales de Mandelbrot et de Julia

Benoît Mandelbrot, 1924-
Gaston Maurice Julia, 1893-1978


Partant de tout point z = x + iy = (x,y), on construit la suite complexe (Zn) par la formule de récurrence :

Z0 = z
Zn+1 = Zn2 + C,

où C=z dans le cas Mandelbrot et C constant dans le cas Julia.
En coordonnées réelles, cela revient donc a construire deux suites (Xn) et (Yn) telles que :

X_0 = x
Y_0 = y

et
Xn+1 = Xn2 −Yn2 + Cx
Yn+1 = 2XnYn + Cy.

où Cx = x et Cy = y dans le cas Mandelbrot, et Cx et Cy sont des constantes dans le cas Julia.
 L'ensemble de Mandelbrot
L'ensemble M de Mandelbrot

Un ensemble de Julia
L'ensemble J(C) de Julia
avec C = 0,72 + 0,11i 		Un ensemble de Julia
L'ensemble J(C) de Julia
avec C = 0,28 − 0,02i
On notera J(C) l'ensemble fractal de Julia de paramètre C, comme défini précédemment. On devrait parler de Julia "plein" ou "rempli" (filled Julia set), car au sens strict l'ensemble de Julia n'est que la frontière ∂J(C) de l'ensemble que nous venons de définir, mais cet abus de langage est fréquent.

On notera M l'ensemble fractal de Mandelbrot. Pour simplifier on dira juste "le Julia" et "le Mandelbrot".

2.2.1.1. Description fine des ensembles de Mandelbrot et Julia
2.2.1.1.1 Propriétés élémentaires des Julia et du Mandelbrot
Remarquons qu'il y une infinité de Julia , un différent pour chaque choix de C. Par contre, il n'y a qu'un seul Mandelbrot. Les Julia ont une forme très autosimilaire : les détails qui apparaissent lorsqu'on zoome le voisinage d'une partie de la frontière sont fortement similaires à l'ensemble entier. L'ensemble de Mandelbrot est sensiblement plus complexe, on peut même en un certain sens le considérer comme une carte, un résumé des Julia : chaque point C du Mandelbrot "ressemble" au Julia de paramètre C.

Plus concrètement, on peut lire directement sur les équations que l'orbite (Zn) du point 0 pour le Julia de paramètre C est exactement la même que l'orbite du point C pour le Mandelbrot (éventuellement, à un décalage d'indice près). Donc, en particulier :
i) Le point 0 appartient à J(C) si et seulement si le point C appartient à M.
Le point 0 est particulier car c'est l'unique point critique de la fonction f(z) = z2 + C (ce qui veut simplement dire que ∂f/∂z(0) = 0), et important à cause d'un résultat dû à Fatou, dont une conséquence est la suivante :

Théorème de Pierre Fatou, 1878-1929
Si un polynôme ou une fraction rationnelle possède un p-cycle stable, alors au moins un des points critiques va converger vers ce cycle.

L'ensemble de Mandelbrot est donc l'ensemble des C tels que la fonction f possède un cycle attracteur (attractive cycle) stable.


Les propriétés suivantes sont des exercices (plus ou moins) faciles :
ii) L'ensemble de Mandelbrot est symétrique par rapport à l'axe des abcisses (axe des réels).
iii) L'ensemble de Mandelbrot est inclus dans le disque fermé centré en 0 de rayon 2.
iv) Chaque ensemble de Julia est symétrique par rapport au point 0 (invariant par rotation de 180°).
v) L'ensemble de Julia J(C) est le symétrique de l'ensemble J(C) par rapport à l'axe des abcisses (où C est le complexe conjugué de C, c'est à dire le symétrique de C par rapport à l'axe des abcisses).
vi) Conséquence immédiate de la propriété précédente : si C=C, autrement dit pour C réel, l'ensemble de Julia J(C) est de plus symétrique par rapport à l'axe des abcisses, donc également symétrique par rapport à l'axe des ordonnées.
vii) L'ensemble de Julia de paramètre C est inclus dans le disque fermé centré en 0 de rayon max(2;|C|).
viii) Pour C=0, l'ensemble de Julia J(0) est le disque fermé centré en 0 de rayon 1.
ix) Pour C=-2, l'ensemble de Julia J(-2) est le segment [-2,0].
2.2.1.1.2 Connexité des Julia et lien avec le Mandelbrot
On sait démontrer que si un Julia ne contient pas 0, alors il n'est pas connexe (il n'est pas fait d'un seul bloc). On peut le comprendre intuitivement, car 0 est le centre de symétrie de tous les Julia. (Donc ce point va être systématiquement absent des répétitions de plus en plus petites de l'ensemble). On appelle ce résultat la dichotomie fondamentale des Julia, il n'y a que deux possibilités : Ainsi en utilisant la "propriété élémentaire" i), on peut dire que

M est formé des points C tels que J(C) est connexe.

Le Mandelbrot peut donc être vu comme une carte de la connexité des Julia. Quand on choisit C à l'intérieur de M, le Julia J(C) est fait d'un seul bloc, d'autant plus large que C est loin de la frontière de M. Pour C sur la frontière, J(C) devient très fin (d'intérieur nul), puis au-delà, pour un C à l'exterieur de M, J(C) est réduit à une poussière de points, d'autant plus fine que C est loin de M.

2.2.1.1.3. Périodes des bulbes du Mandelbrot
Le Mandelbrot peut être assimilé à une sorte carte de l'itération des polynômes complexes du second degré f(z) = az2 + bz + c. Par un changement d'échelle et une translation, on peut se limiter à étudier les polynômes de la forme :
f(z) = z2 + C.
Analysons la stabilité de l'itération de cette fonction au moyen des outils de la section 1.1.2. Tout dépend du seul paramètre complexe C, ce qui va permettre une représentation graphique bidimensionnelle complète.

Pour un point donné C, les points fixes de f vérifient
f(z) = z2 + C = z, soit z2 − z + C = 0,
donc on a deux points fixes α (distincts sauf si C=1/4 ) en fonction de C :
α = 1/2 ⋅ ( 1 ±√ 1 − 4C ).
Etudions la stabilité de ces points fixes, cherchons où sont les points C tels que le module |f′(α)| soit égal à une constante r donnée. En utilisant les coordonnées polaires, écrivons :
f′(α) = r eit     ( pour t∈[0,2π[ et r > 0 ).
Comme f′(z) = 2z,
1±√ 1 − 4C = r eit, soit 1 − 4C = ( r eit − 1 )2,
d'où, en cherchant à regrouper les exponentielles complexes en cosinus,
C = r/2eit − r2/4e2it = r/2eit ( 1 − r/2eit ) = r/2eit ( 1 − r/2eit − r/2e− it + r/2e− it ) = r/2eit ( 1 − r cos t ) + r2/4.
Pour r = |f′(α)| = 1, on obtient l'ensemble des C tels qu'au moins un des points fixes α soit neutre : cette courbe est la frontière entre la stabilité et l'instabilité lors de l'itération de f. En coordonnées polaires centrées en (x,y) = ( 1/4 , 0 ) , cette courbe prend la forme simple :
&rho(t) = 1/2 ⋅ ( 1 − cos t ), pour t∈[0,2π[.
On peut reconnaitre l'équation d'une cardioïde (forme de coeur), qui est la composante principale de l'ensemble de Mandelbrot.

L'intérieur de la cardioïde principale du Mandelbrot M représente les points C tels que les points fixes de la fonction f(z)=z2+C sont stables, donc tels que l'orbite de C sous l'action de f est convergente vers un point fixe. Sur l'axe réel, elle s'étend de x=1/4 à droite (pour t=0) à x=−3/4 (pour t=π). En coordonnées cartésiennes, son équation ( paramétrée par t∈[0,2π[ ) s'écrit :
x(t) = 1/2 ⋅ cos t ⋅ (1 − cos t ) + 1/4,
y(t) = 1/2 ⋅ sin t ⋅ (1 − cos t ).

Pour tout C à l'intérieur de cette cardioïde, donc pour C = r/2eit ( 1 − r cos t ) + r2/4 avec r < 1, les deux points fixes de f sont :
α = r/2eit     et     α = 1 − r/2eit.
Ces points sont stables puisque |f′(α)| = r < 1.


... blablabla ...


La composante principale de l'ensemble de Mandelbrot

La composante principale de M.

Si l'on veut étudier les 2-cycles, il faut s'intéresser à la fonction f itérée 2 fois. En effet, les points 2-périodiques pour f sont les points fixes de f(2), ils vérifient donc :
f(2)(z) = f(f(z)) = ( z2 + C )2 + C = z, soit z4 + 2Cz2 − z + C2 + C = ( z2 − z + C ) ⋅ ( z2 + z + C + 1 ) = 0.
On retrouve le polynôme déjà rencontré f(z) − z = z2 − z + C en facteur, puisque les points fixes sont en particulier 2-périodiques. On a ainsi 4 points solutions, les deux points fixes α déjà calculés, et les deux points périodiques suivants :
β = 1/2 ⋅ ( −1 ±√ −3 − 4C ).
Pour étudier la stabilité de ces points fixes, on s'intéresse à la dérivée de f(2). On a ∂/∂zf(2)(z) = 4z3 + 4Cz = 4z( z2+C ), donc, aux points β,
∂/∂zf(2)(β) = 4β( β2 + C ) = 4β( − β − 1 ) = −4( β2 + β ) = 4( C + 1 ),
car β2+C = − β − 1 et β2 + β = − C − 1 en utilisant l'équation β2 + β + C + 1 = 0. Comme précédemment, on paramétrise l'ensemble des points C tel que les points fixes β sont stables grâce aux coordonnées polaires :
∂/∂zf(2)(β) = r eit, d'où C = −1 + r/4eit.
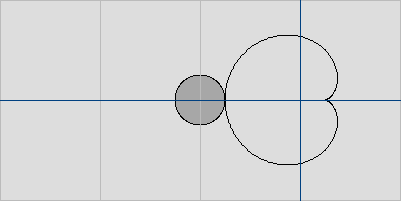
Pour r=1, la limite entre la stabilité et l'instabilité des points fixes pour f(2) est donc un cercle de centre −1 et de rayon 1/4. C'est le plus gros "bulbe" secondaire du Mandelbrot, tangent à la cardioïde en x=−3/4. 		La premiere composante secondaire de l'ensemble de Mandelbrot

La première composante secondaire de M.

On peut continuer indéfiniment de la sorte, et l'étude de chaque fonction f(n)(z)−z nous donnera de nouveaux bulbes représentant les points fixes stables pour f(n), autrement dit les points n-périodiques stables pour f. L'ensemble de Mandelbrot est aussi l'ensemble des valeurs d'adhérences des points fixes ou périodiques, et stables de la fonction f(z)=z2+C. Cependant cette équation se complique extrêmement vite, elle devient rapidement inextricable à la main.

Intéressons-nous à la suite de disques alignés sur l'axe réel, à gauche de la cardïode. Nous avons vu que le premier disque, centré en -1, est exactement l'ensemble des point 2-périodiques (non-fixes) stables pour f. Le disque suivant est un ensemble de points 4-périodiques stables, le suivant correspond à une période de 8, etc.

Ce phénomène de cascade de doublement de période pour les fonction réelles à été étudié en particulier par Feigenbaum. On peut l'observer sur ce diagramme à droite. En abscisse, la valeur de C est ici un nombre réel entre -3 et 1, aligné avec les bulbes du Mandelbrot M des graphes au-dessus, et sur l'axe des ordonnées on a représenté les valeurs d'adhérence (qui sont toutes réelles, entre −2 et 2) de la suite (Zn) obtenue par itération de f.
Ce dessin représente donc le comportement limite des orbites, partant de l'axe réel, c'est à dire de la tranche médiane de M.

On observe nettement le phénomène de doublement de période : cette suite a une limite pour C dans la cardioïde (−0,75 < C < 0,25), deux valeurs d'adhérence dans le premier disque (−1,25 < C < −0,75), quatre valeurs dans le disque suivant, etc.
Quand C diminue, ces doublements sont de plus en plus rapprochés, et d'intensité faible, à tel point qu'ils ont une fin même s'ils sont en nombre infini. En-dessous d'une certain seuil (pour −2 < C < −1,401155...), au-delà de la fin de la suite de disque, les orbites deviennent chaotiques, il y a une infinité de valeurs d'adhérence.
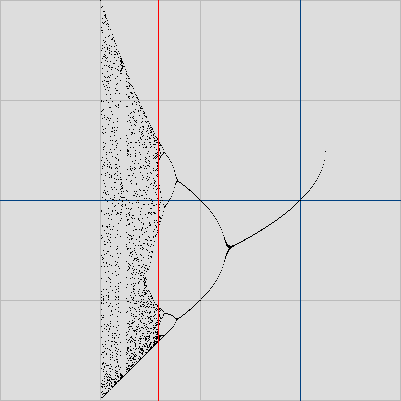
Le diagramme est complet, puisque la suite diverge si C < −2 ou C > 0,25, c'est à dire à l'extérieur de M, dans ce cas il n'y a donc aucune valeur d'adhérence. 		Le diagramme de Feigenbaum associé à x^2+c

Le diagramme de Feigenbaum associé à l'itération de la fonction x→x2+C, pour C∈[-3;1].

La ligne rouge représente la limite de Feigenbaum (C = −1,401155...) entre la cascade de doublements de période et le chaos.
2.2.1.1.4. Quelques points remarquables du Mandelbrot
2.2.1.1.5. Quelques Julia remarquables
2.2.1.2. Un premier algorithme pour tracer les Julia : La méthode d'itération inverse (ou d'orbite inverse)

Connaissant Zn+1 et C, on peut calculer les 2 racines de la formule d'itération de l'ensemble de Julia :
Zn = ±√ Zn+1−C  .
Ces deux points sont deux antécédents possibles pour Zn+1. Partant d'un point quelconque du plan (en général 0), on peut ainsi calculer 2n antécédents en n étapes d'itérations inverse. Les orbites de ces points arrivent en 0 au bout de n étapes, en particulier elles ne fuient donc pas vite à l'infini. On peut montrer que ces points sont denses dans la frontière de J, ils donnent ainsi rapidement une bonne idée graphique de la forme de J (même si le point de départ n'appartient pas au Julia, on peut donc toujours partir de 0).

On commence donc par choisir un n assez grand (en pensant à réserver de la mémoire pour stocker 2n points), puis on pose

Xn+1 = 0   et   Yn+1 = 0.

Pour calculer effectivement la racine à partir de nombres réels, on doit passer par la forme polaire des complexes :
Posons

mn+1 = √  (Xn+1−Cx )2 + (Yn+1−Cy )2         (le module de Zn+1−C, c'est à dire la distance du point (Xn+1−Cx ,Yn+1−Cy ) au centre (0,0) )
et
an+1 = arctg[ (Yn+1−Cy )/(Xn+1−Cx ) ]     (l'argument de Zn+1−C, c'est à dire l'angle entre le vecteur de coordonnées (Xn+1−Cx ,Yn+1−Cy ) et l'axe des abcisses),

on obtient alors deux antécédents (Xn,Yn) et (−Xn,−Yn) avec :

Xn = √  mn+1   ⋅ cos(1/2 an+1)
Yn = √  mn+1   ⋅ sin(1/2 an+1)
Puis on recommence, pour chaque antécédent obtenu. A l'étape suivante (n−1), on obtiendra donc 4 antécédents, puis 8 à l'étape n−2, etc.

Remarquons que cet algorithme ne peut pas être utilisé pour approcher le Mandelbrot.

2.2.2. Ensembles de Mandelbrot et Julia généralisés


On peut généraliser la notion d'ensembles de Mandelbrot et Julia en utilisant un polynôme complexe P quelconque dans la formule d'itération :
Z0 = z
Zn+1 = P(Zn)+C.

Le cas P(Z)=Z2 correspond évidemment aux ensembles de Mandelbrot (C=z) et de Julia (C constant) classique. Pour P polynôme quelconque, on parle de Mandelbrot ou Julia associé à P (dans le cas P(Z)=Zm on parle aussi de Mandelbrot ou Julia généralisé d'ordre m, ou de Mandelbrot puissance m). La relation entre Mandelbrot (C=z) et famille de Julia (C constant) abordée précedemment est toujours vraie.

Par exemple, pour P(Z)=Z3 (on parle alors de Mandelbrot-cube ou de Julia-cube), les formules s'écrivent de la façon suivante en coordonnées réelles :

Xn+1 = Xn3 − 3 Xn Yn2 + Cx
Yn+1 = 3 Xn2 Yn − Yn3 + Cy.

La méthode d'itération inverse s'applique aussi dans ce cadre (mais toujours uniquement pour les Julia) : toute la difficulté est d'arriver à écrire une formule similaire donnant les racines de P (pour P avec un grand nombre de racines distinctes, la formule devient très compliquée).

Evidemment, on peut utiliser d'autres fonction qu'un polynôme, en particulier une fraction rationnelle (quotient de deux polynômes), le mathématicien Julia étudiait notamment l'itération de la fonction
P(Z) = Z4 + Z3/(Z−1) + Z2/(Z3 + 4 Z2 + 5).
On utilise aussi les fonctions dérivées de l'exponentielle complexe, dans ce cas le paramètre C est généralement introduit multiplicativement (plutôt qu'additivement) dans la formule d'itération, par exemple on parle du "Julia de sinus" pour la formule :
Zn+1 = C sin(Zn),
qui s'écrit en coordonnées réelles :
Xn+1 = sin(Xn) * [ (Cx−Cy) exp(Yn) + (Cx+Cy) exp(−Yn) ]
Yn+1 = sin(Xn) * [ (Cx+Cy) exp(Yn) − (Cx−Cy) exp(−Yn) ].
Un ensemble Julia de sinus
L'ensemble Julia de sinus pour C=1+0,1i
Parmi les autres formules couramment utilisées on peut citer :
Zn+1 = C i cos(Zn)
Zn+1 = C exp (Zn)
Zn+1 = C Zn (1 − Zn)
Zn+1 = sin(Zn) + exp(z) + C
Zn+1 = sin(Zn) + exp(C) + z
Les fractales obtenues grâce aux deux dernières formules furent appelées "biomorphs" par C.A. Pickover.

2.2.3. Les fractales de Newton

Sir Isaac Newton, 1642-1727


Newton savait que tout polynôme complexe P de degré m, c'est à dire une fonction de la forme
P(Z)= a0 + a1Z + a2Z2 + ... + amZm,
a au plus m racines dans C. Mais quand m est grand, trouver les racines de P (les points où P s'annule, on dit aussi les zéros de P) en fonction des coefficients a0, ... ,am devient vite un problème inextricable, et Newton a inventé un algorithme de recherche des racines. Il construisait une suite (Zn) par la formule :

Z0 = z
Zn+1 = Zn − P(Zn)/P′(Zn).
Partant d'un z "bien choisi", la suite (Zn) converge vers une racine de P.
On appelle ensemble fractal de Newton associé à P, noté N(P), l'ensemble fractal associé à cette formule d'itération. Sa forme semble tissée entre les racines de P. Remarquons qu'on peut prendre n'importe quelle fonction (holomorphe et possédant au moins deux racines de préférence) à la place de P.
L'exemple classique est P(Z) = Zm − 1, qui a m racines disposées en rond sur le cercle unité (et comme lorsqu'on compose un bouquet de fleurs, choisir un nombre m impair aboutira à une agréable assymétrie...).
Par exemple, pour P(Z)=Z3−1, les formules s'écrivent de la façon suivante en coordonnées réelles :

Xn+1 = Xn − ( Xn5 − 10 Xn3 Yn2 + 5 Xn Yn4 − Xn2 + Yn2 )/3( Xn4 + 4 Xn2 Yn2 + Yn4 )
Yn+1 = Yn − ( 5 Xn4 Yn − 10 Xn2 Yn3 + Yn5 − 2 Xn Yn )/3( Xn4 + 4 Xn2 Yn2 + Yn4 ).
Un ensemble de Newton

L'ensemble N(P) de Newton
avec P(Z)=Z5−1
On peut évidemment mélanger le principe du Mandelbrot et du Newton en considérant
Zn+1 = Zn − P(Zn)/P′(Zn) + C     ou encore     Zn+1 = Zn − C ⋅ P(Zn)/P′(Zn).

Haut de page - Page précédente : - Page suivante : - - Sommaire - Notations

Références

Livres et articles

[Bar88] "Fractals Everywhere", Michael Barnsley, Academic Press, San Diego, 1988.

[CEJ91] "Fractals and chaos", A. J. Crilly, R. A. Earnshaw, H. Jones, editors, Springer-Verlag, New York, 1991.

[CM89] "Complex Universality" de Cvitanovic et Myrheim, Comm. Math. Phys. 121, 225-254 (1989)

[Dev89] "An Introduction to Chaotic Dynamical Systems", R. Devaney, Addison-Wesley, 1989.

[DK89] "Chaos and fractals: the mathematics behind the computer graphics", Robert L. Devaney, and Linda Keen, editors, American Mathematical Society, Providence, RI, 1989.

[Fei80] "Universal Behavior in Nonlinear Systems" Feigenbaum M.J., Los Alamos Science 1, 4-27 (1980)

[FR92] "A Generalized Mandelbrot Set and the Role of Critical Points", M. Frame and J. Robertson, Computers and Graphics 16,No. 1 (1992), pages 35-40.

[Gle87] "La théorie du chaos : vers une nouvelle science" de James Gleick, traduit par Christian Jeanmougin (1999) (original : "Chaos : Making a New Science", Viking Press, New York, 1987)

[Jul18] "Mémoire sur l'itération des fractions rationnelles" de Gaston Julia, Journal de Mathématiques Pures et Appliquées, No. 8 (1918), pages 47-245

[JPS92] "Chaos and Fractals: New Frontiers of Science", H. Jürgens, H.-O. Peitgen, and D. Saupe, Springer, New York, 1992.

[Man75] "Les objets fractals : forme, hasard et dimension, survol du langage fractal" de Benoît Mandelbrot (1975)

[Man77] "The Fractal Geometry of Nature", B. B. Mandelbrot, Freeman, New York, 1977, 1982, 1983.

[PR86] "Beauty of Fractals: Images of Complex Dynamical Systems" de Heinz-Otto Peitgen et Peter H. Richter Springer, Berlin, New York, Tokyo (1986)

[PS89] "The Science of Fractal Images", H.-O. Peitgen and D. Saupe, Springer, Berlin, New York, 1989.

[H94]"A First Course in Discrete Dynamical Systems", R. Homlgren, Springer-Verlag, 1994.

Pages web

Un magnifique PDF sur la génération des fractales
Sur la coloration
Sur la coloration (nombreux liens)
Sur la coloration avec une texture
Lina's Art Gallery - Images et considérations mathématiques
Sur les lignes de champs
Benoît Mandelbrot
Benoît Mandelbrot (autre)
Gaston Julia
The Mandelbrot Set and Julia Sets
An introduction to fractals
Complex Analysis
A virtual investigation with interactive pictures : The Mandelbrot and Julia sets Anatomy and Chaotic dynamics (autre lien), références.
Fractal Frequently Asked Questions and Answers
A short walk through the Mandelbrot Set
Vocabulaire combinatoire de l'imagerie fractale (PDF)

Last modification : John Bonobo @ Thu 18 Mar 2004, 03:03:08.
Cette page respecte les standards définis par le W3C.